Symbolic Expression Graph

Program: Represented In SSA Form

First, multiple assignments to the same variable are distinguished by introduing different versions of the variable and renaming the relatated assignments:

x = 10
y = x + 5
x = 20
z = x + y

// In SSA form, it would be represented as:

x1 = 10
y1 = x1 + 5
x2 = 20
z1 = x2 + y1

Second, at the merge point of different control flow paths, a special statement called phi-assignment is introduced to merge the values of variables from different paths:

if (x < 10) {
  y = x + 5;
} else {
  y = x - 5;
}
z = y * 2;

// In SSA form, it would be represented as:

if (x1 < 10) {
  y1 = x1 + 5;
} else {
  y2 = x1 - 5;
}
y3 = phi(y1, y2); // phi-assignment to merge y1 and y2
z1 = y3 * 2;

Here, the phi-assignment is used to merge the values of “y1” and “y2” from different control flow paths. The phi-assignment takes as inputs a set of variables and their corresponding definitions from different paths and introduces a new version of the variable that represents the merged value.

SEG: Compact Graph Encoding of the Program Dependencies

Simply put, SEG connects value definitions to their uses, while being aware of the semantics of arithmetic computations and pointer operations. Each function has its own SEG, while procedural calls and returns are modeled through special “conduits” connecting multiple SEGs. We first dicuss how SEG encodes direct data dependencies within a single function and then illustrate the handling of indirect or inter-procedural data dependencies.

Direct Data Dependencies

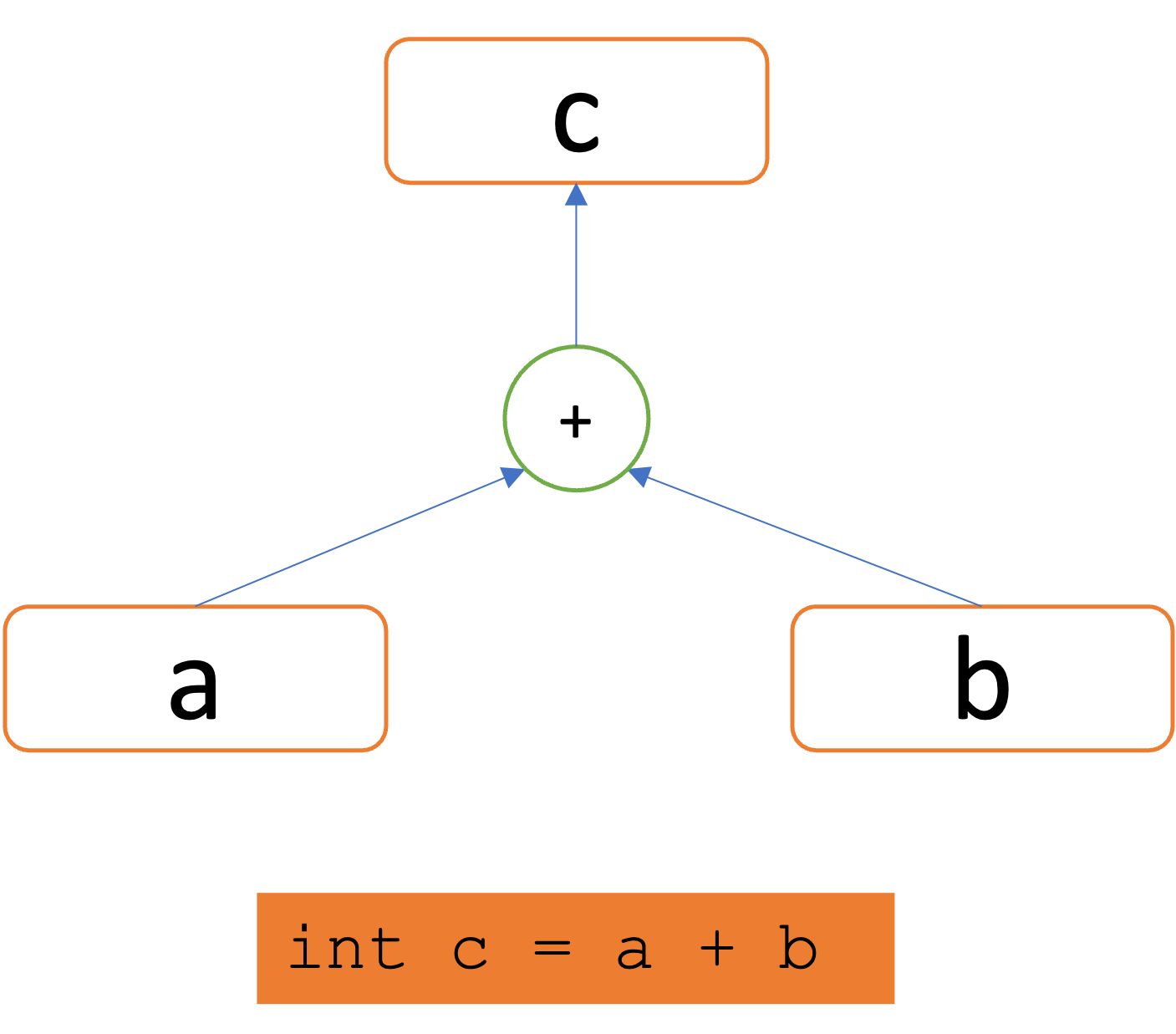
As an example, the above figure shows the statement int c = a + b and its representation in SEG (here only data dependencies are relevant). Notably, nodes labeled with a, b, c correspond to the values a, b, c respectively, while the node labeled with + represents the intermediate computation result a+b. SEG nodes are connected by value flow edges, e.g., the edge a -> + indicates that the computation result a+b is data dependent on a (or the value of a flows to a+b). Notice that our adoption of the SSA form enables us to label the SEG nodes with variable names as they uniquely identify their values.

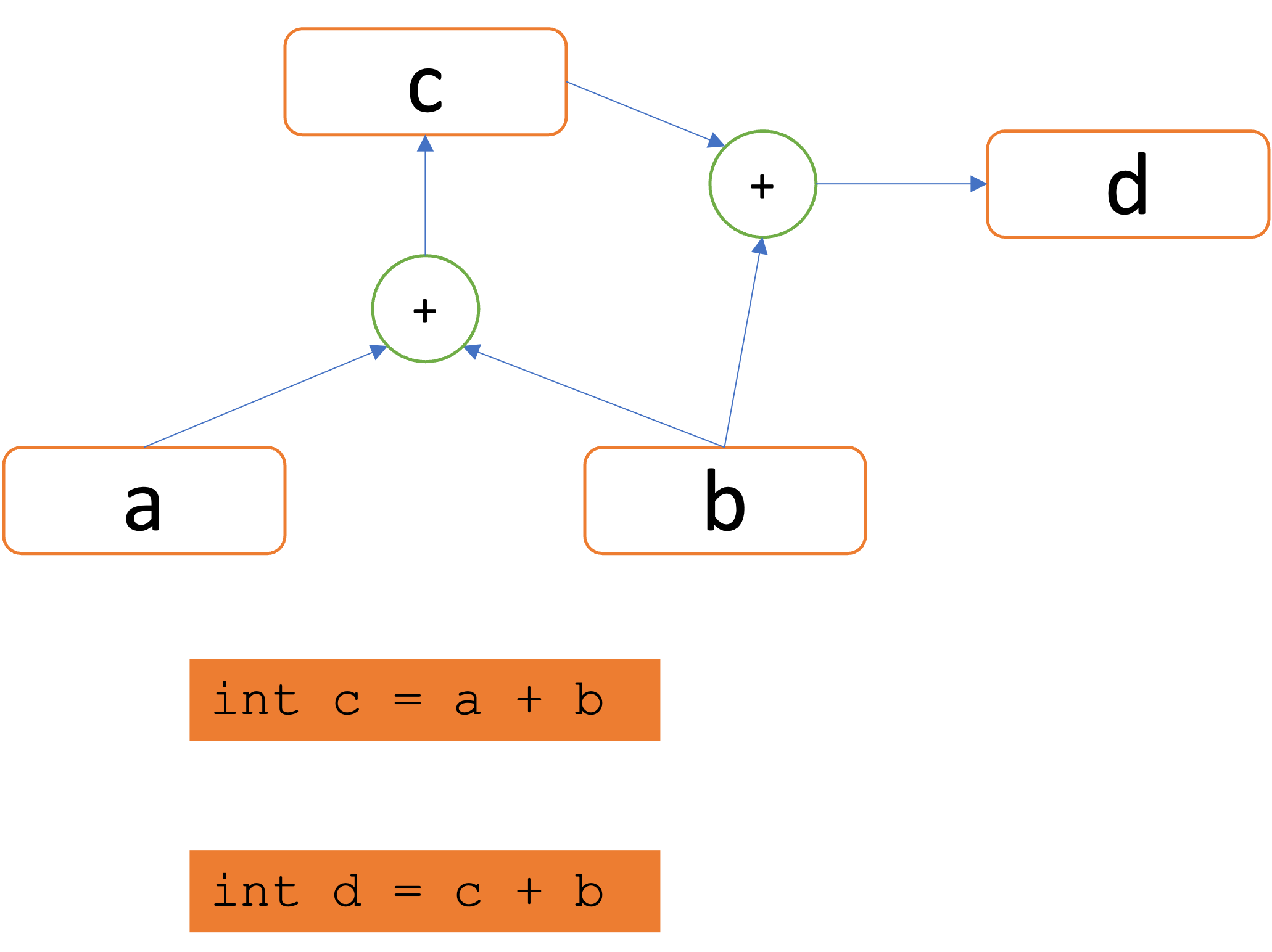
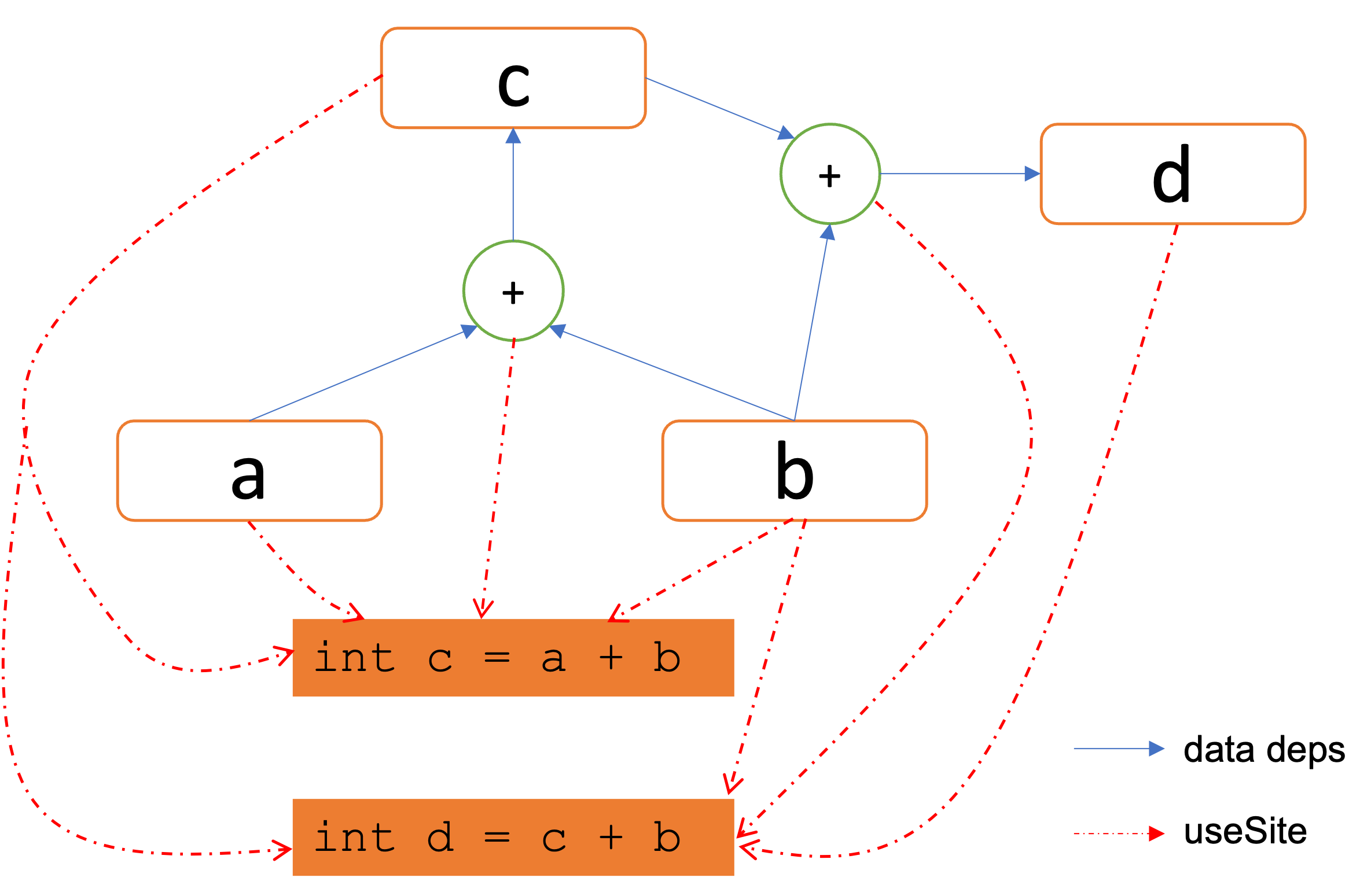
The SEG structure is compact because its nodes are maximally shared: Adding a new instruction int d = c + b will cause the SEG to share the nodes for c and b as shown above. Because a single SEG node can be shared by multiple instructions from the program, we introduce a new type of use site edge that connects a SEG node to all the instructions that use its value, which is represented by the red dashed edges below:

Indirect Data Dependencies

In real programs, a value could be first stored into the heap memory and later retrieved through loading a pointer pointing to the stored location, which creates an indirect data dependency between the load and store statements. We illustrate how SEG handles such indirect data dependencies with the following example.

int a = 5, b = 6;
int *c = malloc(...); // assert c != null
if (a > 0) {
  *c = a;
} else {
  *c = b;
}
int *d = c;
int e = *d;

In the code above, the value of a or b is first stored into the heap via the pointer c and later retrieved into e by loading the pointer d, where d and c are aliases to the same memory location. Our SEG for the above function is:

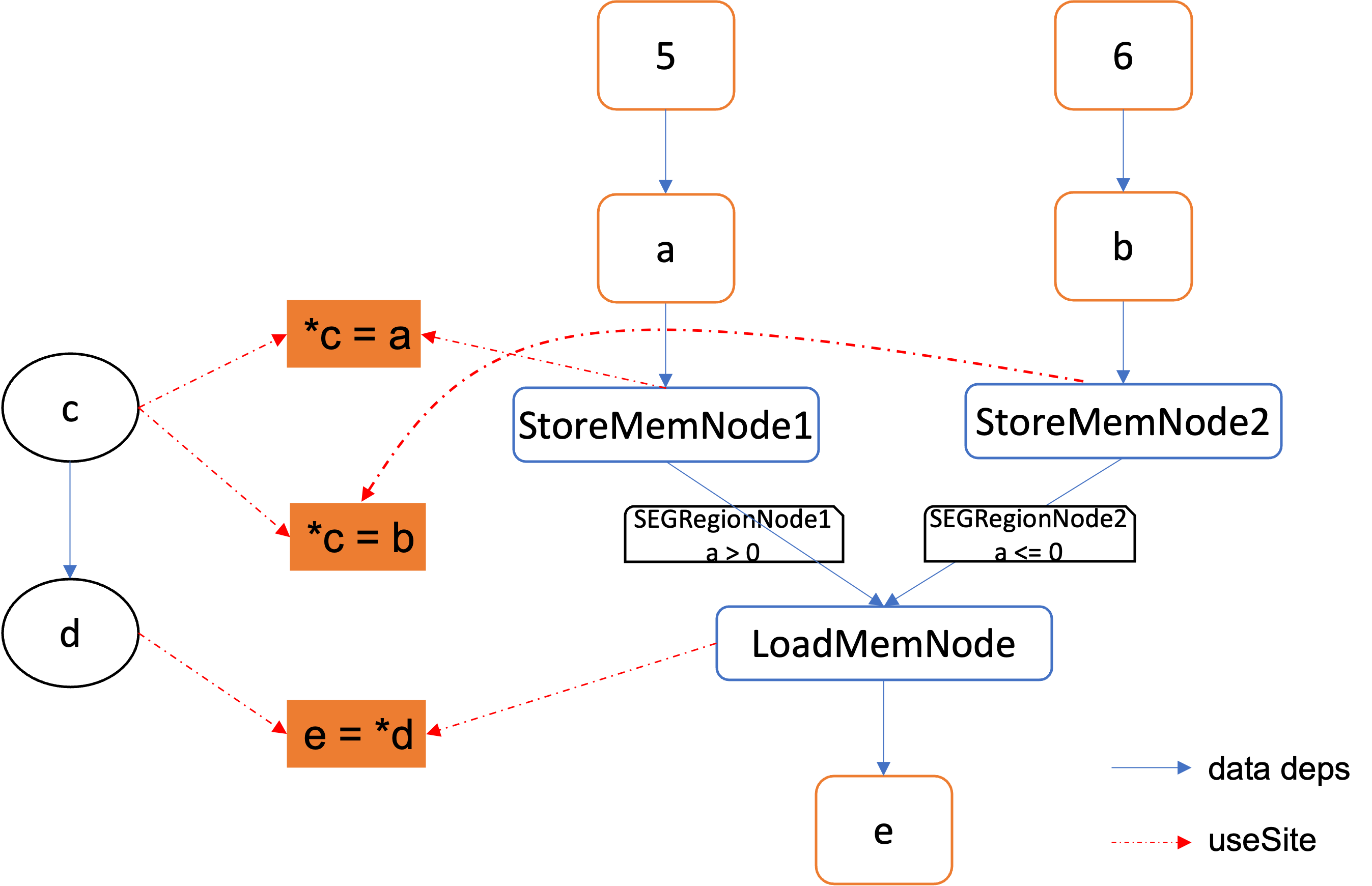
We highlight several important points:

1. We introduce a special type of node called StoreMemNode to denote the value *c that is contained in the stored heap location. Similar to SSA, multiple stores to c cause the StoreMemNode to take different versions as in StoreMemNode1 and StoreMemNode2.
2. We introduce a special type of node called LoadMemNode to denote the value *d that is loaded from a heap location.
3. We figure out the possible values a LoadMemNode could take by matching it with StoreMemNode. In this example, both StoreMemNode1 and StoreMemNode2 could flow to the LoadMemNode. Technically, the matching is computed by applying a pointer analysis: If the involved pointers (c and d in our example) are possible to point to the same memory location, SEG matches the corresponding StoreMemNode and LoadMemNode. We refer the readers to the literature of pointer analysis for more details.

Control Dependencies and Path-sensitivity

Recall that control dependency is related to the branch conditions necessary for a certain program location to be reachable. In the above example, the value of a flows into e only when a > 0, i.e., the true branch of the if statement must be taken. This information is encoded compactly using a label (which we call a RegionNode) on value flow edges.

By concatenating the labels of a sequence of value flow edges, we can recover the complete control dependencies for a specific value flow to occur. In this manner, our analysis is path-sensitive for distinguishing the different execution paths and conditions. For instance, the value flow path 6-> b -> StoreMemNode2 -> LoadMemNode -> e is not feasible because the condition a<=0 is false. We can thus infer that e cannot take the value of b.

Dependencies Across Function boundaries

The handling of function calls and returns is crucial for propagating data depdenencies inter-procedurally. Consider the following code:

int foo(int x, int *p1, int *p2) {
  int actual_ret = x + (*p1);
  *p2 = actual_ret;
  return actual_ret;
}

void bar() {
  int actual_output;
  int *a1 = (int *) malloc(sizeof(int));
  *a1 = 2;

  int *a2 = (int *) malloc(sizeof(int));
  actual_output = foo(1, a1, a2);
  ...
}

At the call statement foo(1, a1, a2) inside the caller function bar, we should (1) propagate direct data dependencies: values should propagate from the actual arguments (1, a1, a2) to the formal parameters (x, p1, p2), and from the return value (actual_ret) to the call site output variables (actual_output). (2) propagate indirect data dependencies: as the function parameters could be pointers, the called function may load or store through the parameters and cause side-effects.

Clearblue handles (2) by introducing pseudo variables to make the side-effects (i.e., reading from *p1 and writing into *p2) explicit. Conceptually, the above code is equivalent to the following “pure” version:

int foo(int x, int *p1, int *p2, int pseudo_arg) {
  int actual_ret = x + pseudo_arg; // pseudo_arg should equal *p1 before the call
  int pseudo_ret = actual_ret; // *p2 should store pseudo_ret after the call
  return (actual_ret, pseudo_ret);
}

void bar() {
  int actual_output, pseduo_output;
  int *a1 = (int *) malloc(sizeof(int));
  *a1 = 2;

  int *a2 = (int *) malloc(sizeof(int));
  int psedo_input = *a1; // representing memory read in foo
  (actual_output, pseduo_output) = foo(1, a1, a2, psedo_input);
  *a2 = pseduo_output; // representing memory write in foo
  ...
}

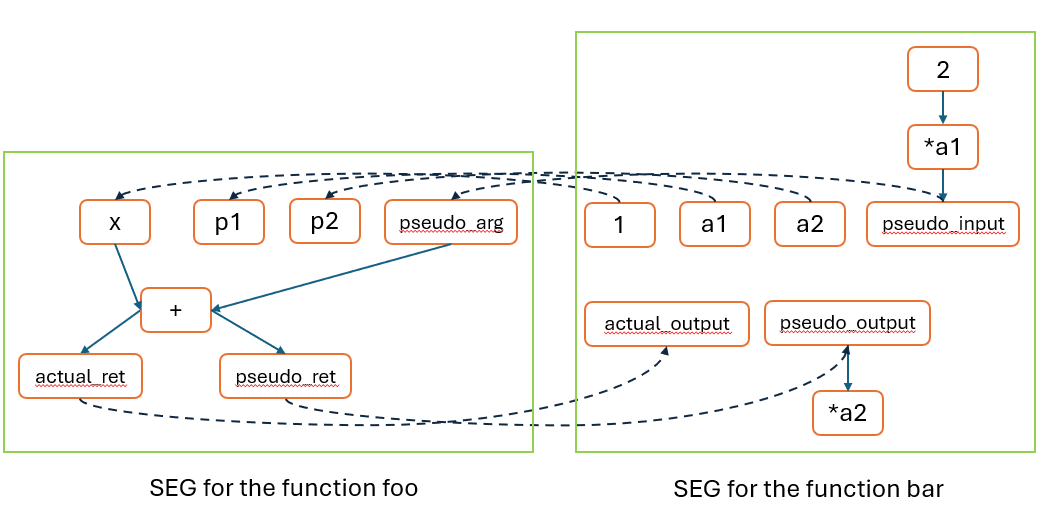
The above graph depicts the individual SEGS for the function foo and bar, while the inter-procedural data depdenencies between the caller and the callee are represented by the dashed arrows. In Clearblue, we directly construct the above SEGs without actually transforming a program to its pure counterpart. The SEG nodes that are involved in inter-procedural analysis deserve some special care. They form the conduits of inter-procedural value flow and can be classified into eight types.

1. SEGCommonArgument: the formal parameters of a function, such as x, p1, p2.
2. SEGPseudoArgument: the introduced auxiliary formal parameter representing values read by the function, such as pseudo_arg.
3. SEGCommonInput: the actual values passed to SEGCommonArgument at a given call site, such as 1, a1, a2.
4. SEGPseduoInput: the actual values passed to SEGPseudoArgument at a given call site, such as pseudo_input.
5. SEGCommonReturn: the return value of a function, such as actual_ret.
6. SEGPseudoReturn: the introduced auxiliary return value representing values written by the function, such as pseudo_ret.
7. SEGCallSiteCommonOutput: the receiver variable for SEGCommonReturn at a given call site, such as actual_output.
8. SEGCallSitePseudoOutput: the introduced auxiliary receiver variable for SEGPseudoReturn at a given call site, such as pseudo_output.